Wróbel Agata
Department of Theoretical and Structural Chemistry
Laboratory of Crystallochemistry
Experimental Electron Density Distribution and QTAIM Topological Analysis for the Perovskite Mineral: Sulphohalite – Na6(SO4)2FCl
Agata Marta Wróbel
Supervisor: prof. dr hab. Krzysztof Woźniak, dr Roman Gajda
The acquaintance of modern crystallography onto mineralogy will be approached by endeavouring in an experimental charge density study for the double antiperovskite mineral – sulphohalite [Na6(SO4)2FCl]. A crystal of suitable quality was encountered in a mineral sample proceeding from Sears Lake, California, USA. Chemical composition and purity were evaluated through EDS analysis. High-resolution X-ray diffraction data was collected employing AgKα radiation (λ = 0.56087 Å) to a resolution of 0.3941 Å at 100K. The crystal structure was solved by direct methods implementation based on merged SHELX[1] data – in compliance with the Independent Atom Model (IAM). Electron density (ED) distribution – ρ(r) was modelled, as proposed in the Hansen-Coppens formalism[2], by consecutive least-square multipolar refinements. The quality of collected data and computed ED model were assessed by means of DRK[3], normal probability[4] and fractal dimension plots[5]. Conclusively, they were found to be of good quality.
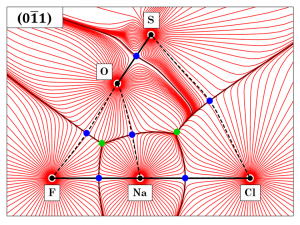
Fig 1. Gradient vector field of the total ED distribution in the crystal of sulphohalite – plotted onto the (0-11) plane. Interatomic bonding is presented by black lines; whereas bonding paths are depicted by black dashed lines. Bond CP’s – (3, -1) and Ring CP’s – (3, +1) are respectively denoted by blue and green circles.
QTAIM topological analysis[6] was undertaken based on the experimentally attained distribution of charge. Atomic basins (AB’s) were delineated based on the zero flux surfaces (ZFS’s) denoted on the gradient vector field of ED – ∇ρ(r). The appertaining volumes and charges of each basin were computed by full-volume integration. Following, critical points (CP’s) were identified as local extrema of the ∇ρ(r) function, and classified based on the Laplacian of ED – ∇2ρ(r). Morse’s ‘characteristic set’ condition was met[7]. The study of primary bundles (PB’s), as proposed by Pendás et al.[8], revealed the interconnection between AB’s and CP’s onto basins of attraction or basins of repulsion. The nature of interatomic interactions was assessed through the dichotomous classification[7]. The S–O contact was acknowledged as a covalent with a shared-shell. The remaining contacts were characterized as non-covalent closed-shell (Cl···Na, Na···O and Na···F) or weak van der Waals closed-shell (Cl···S and F···O).
References:
[1] G. M. Sheldrick, ‘A short history of ıt SHELX’, Acta Crystallographica Section A, vol. 64, no. 1, pp. 112–122, Jan. 2008, doi: 10.1107/S0108767307043930.
[2] N. K. Hansen and P. Coppens, ‘Testing aspherical atom refinements on small-molecule data sets’, Acta Crystallographica Section A, vol. 34, no. 6, pp. 909–921, Nov. 1978, doi: 10.1107/S0567739478001886.
[3] A. Stash, DRK plot for XD and SHELX. Moscow, 2007.
[4] V. V. Zhurov, E. A. Zhurova, and A. A. Pinkerton, ‘Optimization and evaluation of data quality for charge density studies’, Journal of Applied Crystallography, vol. 41, no. 2, pp. 340–349, 2008, doi: https://doi.org/10.1107/S0021889808004482.
[5] K. Meindl and J. Henn, ‘Foundations of residual-density analysis’, Acta Crystallographica Section A, vol. 64, no. 3, pp. 404–418, May 2008, doi: 10.1107/S0108767308006879.
[6] R. Bader, Atoms in Molecules: A Quantum Theory. USA: Oxford University Press, 1994.
[7] ‘Chemical bonding in crystals: new directions’, Zeitschrift für Kristallographie – Crystalline Materials, vol. 220, no. 5–6, pp. 399–457, 2005, doi: doi:10.1524/zkri.220.5.399.65073.
[8] A. Martín Pendás, A. Costales, and V. Luaña, ‘Ions in crystals: The topology of the electron density in ionic materials. I. Fundamentals’, Phys. Rev. B, vol. 55, no. 7, pp. 4275–4284, Feb. 1997, doi: 10.1103/PhysRevB.55.4275.